Lineare Funktionen

Eine lineare Funktion ist eine Funktion $f:\mathbb{R} \rightarrow \mathbb{R}$ mit einer Gleichung der Form
$y = f(x) = mx +q$
$m,q \in \mathbb{R}$

Steigung

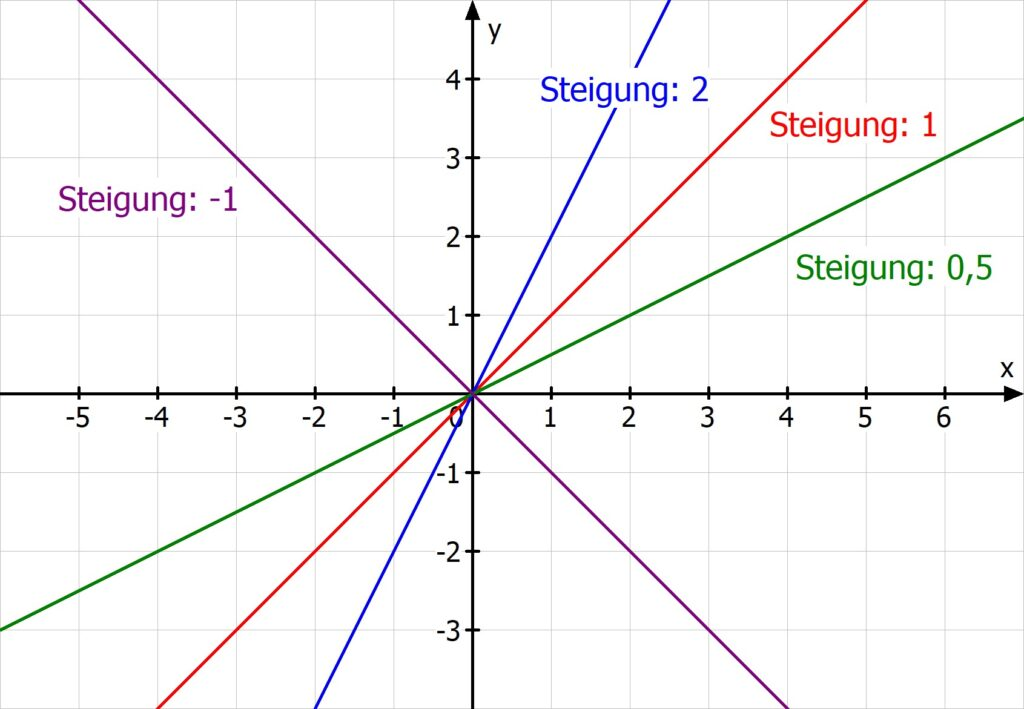
Lineare Funktionen mit der Gleichung $y = mx$ gehen immer durch den Ursprung (0;0). Mann nennt sie deshalb auch Ursprungsgeraden.

Das Verhältnis $\frac{y}{x} =m$ ist konstant.

Der Faktor m bestimmt die Steigung der Funktion. Von ihm häng ab, ob die Geraden steigen oder fallen und wie steil oder flach sie Verlaufen.

Ordinatenabschnitt

Lineare Funktionen mit der Gleichung $y=mx+q$ gehen nicht mehr durch den Urpsrung.
Zu jedem Funktionswert $y$ wird der konstante Wert $q$ addiert.

Dadurch verschiebt sich die $y$-Achse genau um den Wert von $q$.

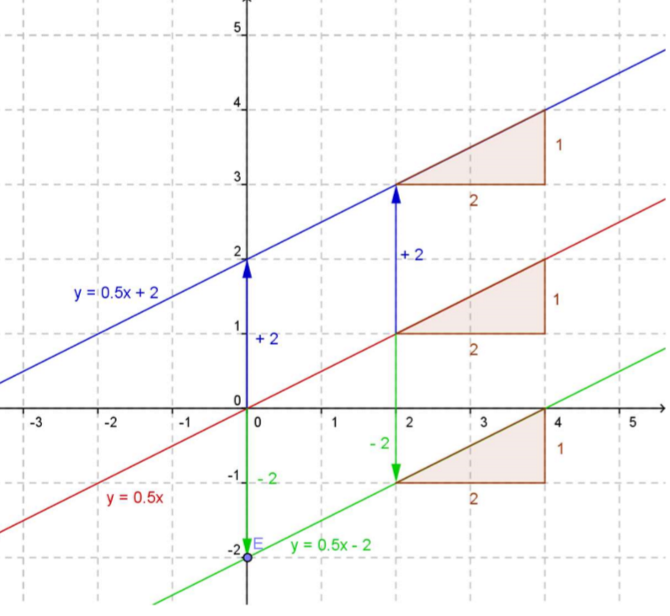
Für die Verschiebung gilt:

• $q \gt 0$, der Graph verschiebt sich nach oben
• $q \lt 0$, der Graph verschiebt sich nach unten

Der Wert des Parameters kann im Graphen direkt beim Schnittpunkt mit der $y$-Achse abgelesen werden, also bei x = 0.

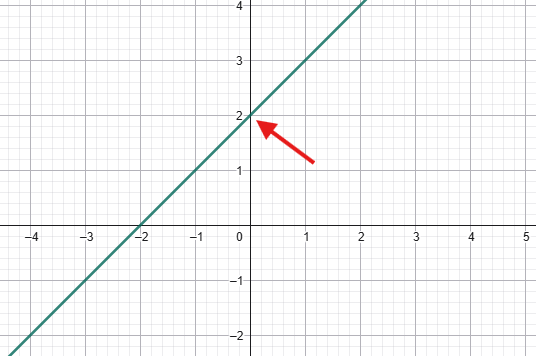
In diesem Beispiel ist $q$= 2, da bei x = 0, y = 2 ist. (0;2)

🤓 Die Variabel wird als Absolutglied oder eben Ordinatenabschnitt bezeichnet!

Steigung berechnen

Um die Steigung eines graphes zu berechnen, erstellt man aus 2 bestehenden Punkten ein rechtwinkliges Dreieck. Die Steigung kann dann aus den geraden $\frac{a}{b}$ berechnet werden. Genauer gesagt einfach mit der Formel $m = \frac{\Delta y}{\Delta x} = \frac{y_2 – y_1}{x_2 – x_1}$

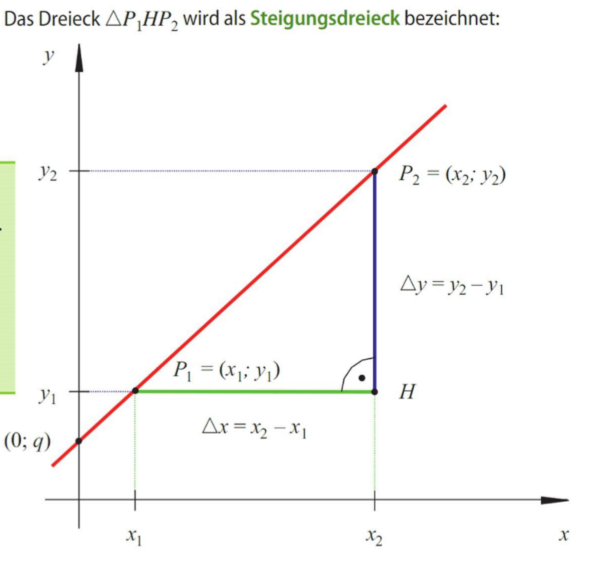
$a$ kann berechnet werden, in dem man in die Gleichung $y = mx +q$ einen Punkt einsetzt.
Zum Beispiel bei $(3;5)$ wäre dann die Gleichung

Schnittpunkte

Die Nullstelle ist an der Stelle, an der $y = 0$ ist.
Wir können in der Gleichung also einfach $y = 0$ einsetzen, wodurch wir dann $x$ berechnen können.

Nullstelle $\neq$ Schnittpunkt

• Schnittpunkt -> der Punkt, an dem X = 0 ist
• Nullstelle -> wenn der Punkt y = 0 ist

Schnittpunkte zweier Geraden

Wenn sich zwei Graden Schneiden, erfüllt die Koordinaten des Schnittpunktes beide Funktionsgleichungen.

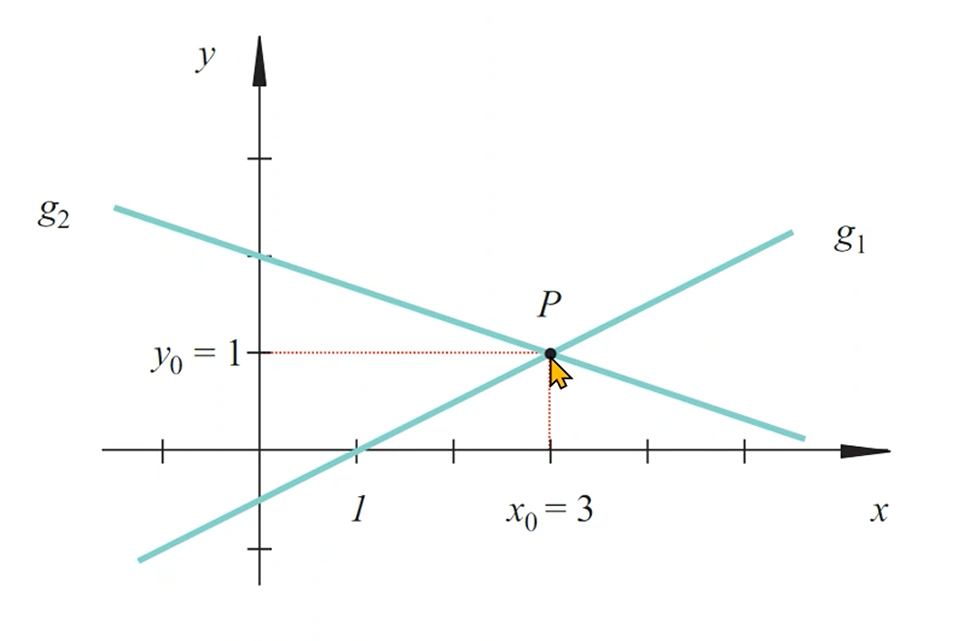
Dies entspricht einem Gleichunssystem mit 2 unbekannten

Parallele Geraden

Zwei Geraden sind parallel, wenn sie die gleiche Steigung haben.

Sie haben den selben Neigungswinkel, schneiden sich also nie (ausser sie sind identisch).

Senkrechte Geraden

Zwei Geraden sind senkrecht (rechtwinklig oder auch orthogonal) zueinander, wenn sie sich unter einem Winkel von $90\degree$ schneiden.

Für ihre Steigung gilt:

Also wenn wir die Steigung $m_1 = 3$ haben, wäre: $m_2 = -\frac{1}{3}$

Mittelparallelen

Wenn zwei Geraden parallel sind, kann man die Mittelparallele bestimmen. Das ist eine Gerade, die genau in der Mitte zwischen beiden liegt und die gleiche Steigung hat.

Wenn wir folgende Geraden $g$ und $h$ haben:

Dann gilt die Formel für die Mittelparallele