Quadratische Funktionen

In diesem Beitrag findest du eine übersichtliche Zusammenfassung zu quadratischen Funktionen aus der BM2. Ich habe diese ursprünglich für mich zum lernen erstellt, vielleicht hilft sie ja auch dir!
Aus diesem Grund kann es jedoch gut sein, dass die Zusammenfassung unvollständig und durcheinander wirkt.

Übersicht

• Allgemein Form quadratischer Funktionen
• Scheitelform
• Streckung / Stauchung
• Verschiebungen
• Schnittpunkte

Allgemein

Eine quadratische Funktion hat die allgemeine Form:

$a$ darf dabei nicht 0 sein, da wir sonst einfach eine lineare Funktion hätten.
-> Der Graph einer quadratischen Funktion wird Parabel genannt.

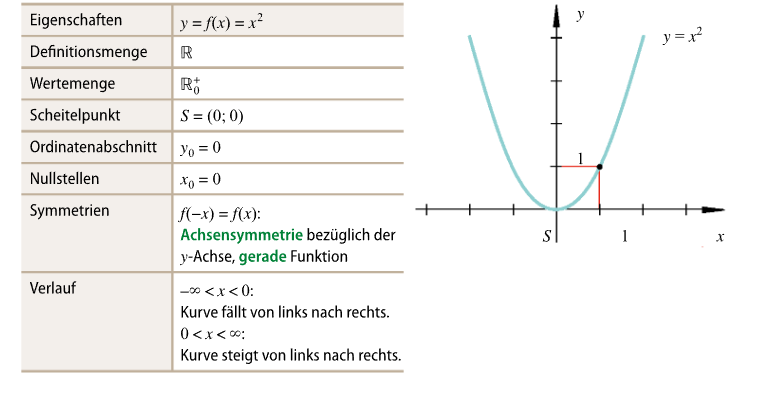
Normalparabel

Die einfachste quadratische Funktion lautet $y=x^2$
Diese nennt man “Normalparabel”

Scheitelform der quadratischen Funktion

Für die Berechnung der Funktionsgleichung können wir die Scheitelform verwenden:

Wir müssen lediglich den Scheitelpunkt + einen beliebigen Punkt aus der Parabel kennen.

In der Formel wird der Scheitelpunkt bei $u$ und $v$ eingesetzt → $S = (u,v)$
$x$ und $y$ kann durch den zweiten bekannte Punkt eingesetzt werden, wodurch wir dann $a$ berechnen können.

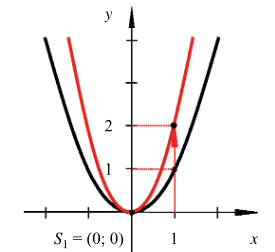
Streckung / Stauchung

Bei der quadratischen Grundform bestimmt die variabel $a$, die Streckung oder Stauchung der Parabel. Wenn wir $a=2$ einsetzen, wird die Parabel nach oben gestreckt

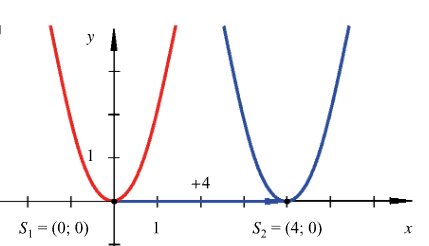
Horizontale Verschiebung

Um die Parabel horizontal auf der $x$ Achse zu verschieben, verwenden wir einen Teil der Scheitelform.

Wenn wir also die Parabel um 4 stellen nach rechts verschieben wollen, setzen wir als Ursprung $S_2=(4;0)$in der Formel $y = a(x-u)^2$ein und erhalten:

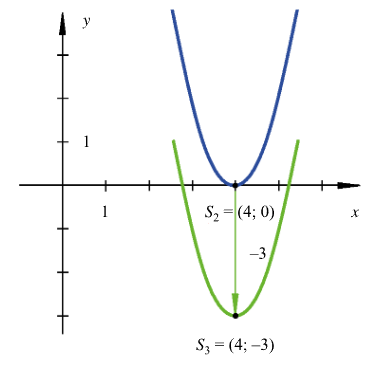
Vertikale Verschiebung

Wir können die Parabel auch noch vertikal verschieben. Dafür müssen wir lediglich $v$ in der Scheitelform verändern. Wenn wir also neu den Scheitelpunkt $S=(4;-3)$ haben, lautet die neue Scheitelform:

Von der Grundform zum Scheitelpunkt

Wir wollen nun aus einer quadratischen Funktion den Scheitelpunkt berechnen. Wenn bereits die Scheitelform gegeben ist können wir den Scheitelpunkt einfach auslesen. Aus der Grundformel $y=ax^2+bx+c$ nicht.

Um den Scheitelpunkt $S=(u;v)$ zu berechnen verwenden wir folgende beiden Formeln:

Warum geht das so?

 Wenn wir die Scheitelform $y=a(x-u)^2+v$ mit der binomischen Formel aus multiplizieren, erhalten wir:

Funktionsgleichung aus den Nullstellen

Wenn wir die Nullstellen und gegeben haben, gilt:

Somit können die Punkte in folgende Formel eingetragen werden:

Ausmultipliziert würden wir dann wieder in die Grundform kommen.

Der Wert des Scheitelpunktes liegt aus Symmetriegründen immer in der Mitte der beiden Nullstellen und . Daraus ergibt sich:

Für die Grundform gilt dann also:

Schnittpunkte mit den Koordinatenachsen

Schnittpunkt mit der y-Achse

Der Schnittpunkt mit der y-Achse ist dort, wo ist. Also theoretisch wie in den quadratischen Funktionen der Ordinatenabschnitt. Wenn

Wenn wir in die Grundform einer Quadratischen Funktion einsetzen erhalten wir Somit ist der Schnittpunkt mit der y-Achse immer:

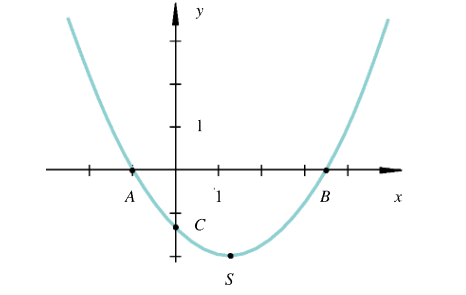
Schnittpunkt mit der x-Achse

Der Schnittpunkt mit der x-Achse (Nullstelle) ist dort, wo gilt. Wir lösen also einfach die quadratische Gleichung

Dafür können wir einfach die Mitternachtsformel verwenden:

Der Ausdruck unter der Wurzel ist die Diskriminante. An dieser können wir auslesen, wie viele Nullstellen die Parabel hat.

• → 2 Nullstellen
• → 1 Nullstelle
• → keine Nullstelle